Le reti neurali artificiali sono modelli matematici non lineari utilizzati per rappresentare e simulare relazioni complesse tra ingressi e uscite, laddove altre funzioni analitiche risultano insufficienti.

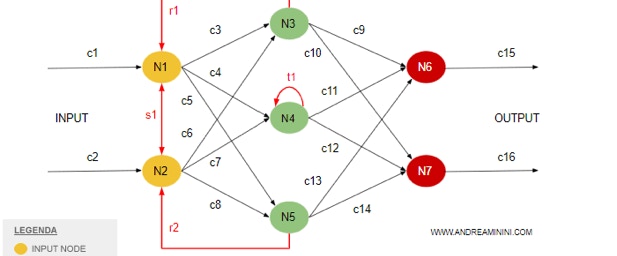
Come accennato nell’introduzione, una rete neurale riceve segnali esterni attraverso uno strato di nodi di ingresso (unità di elaborazione). Questi nodi sono connessi a numerosi nodi interni, organizzati in più livelli. Ogni nodo elabora i segnali ricevuti e trasmette il risultato ai nodi successivi, contribuendo così al processo di apprendimento e modellazione dei dati.

Funzioni discriminanti

Una funzione discriminante è un modello matematico che, a partire dai dati in ingresso, fornisce in output una classificazione di tali dati. L’esempio più semplice è una combinazione lineare delle variabili di ingresso.

Questo modello di base può essere generalizzato applicando una funzione di attivazione, che introduce una trasformazione non lineare nel risultato, rendendo la funzione discriminante più flessibile e capace di rappresentare relazioni più complesse.

Consideriamo un problema di classificazione binaria, in cui i dati devono essere assegnati a una delle due classi, C₁ e C₂. In questo caso, una funzione discriminante y(x)  può determinare l’appartenenza del vettore x a una classe specifica secondo la seguente regola:

    •    x appartiene a C₁ se y(x) > 0 

    •    x appartiene a C₂ se y(x) < 0 

La funzione discriminante più semplice ha la forma:

y(x, w) = w^T x + w_0

Dove:

    •    w è un vettore di pesi,

    •    w₀ è un termine di bias,

    •     w^T x  rappresenta il prodotto scalare tra il vettore dei pesi e il vettore di ingresso.

1. Funzione Discriminante Lineare

Un problema di classificazione binaria può essere risolto con una funzione discriminante y(x) , che separa le classi  C_1  e  C_2  secondo:

    •     x \in C_1  se  y(x) > 0 

    •     x \in C_2  se  y(x) < 0 

La funzione discriminante più semplice è lineare:

y(x) = w^T x + w_0

Dove w  è un vettore di pesi e  w_0  è un termine di bias. Geometricamente, il confine decisionale  y(x) = 0  è un iperpiano di dimensione  (d-1) , con  w  normale all’iperpiano. La distanza dall’origine è data da  |w_0| / ||w|| .

2. Estensione a più classi

Per più classi, si introduce una funzione discriminante per ciascuna classe C_k :

y_k(x) = w_k^T x + w_{k0}

Il punto x  viene assegnato alla classe con il valore massimo di  y_k(x) . Il confine tra due classi  C_k  e  C_j  è un iperpiano dato da:

(w_k - w_j)^T x + (w_{k0} - w_{j0}) = 0

Le regioni di classificazione risultano insiemi convessi.

3. Funzioni di Attivazione

Invece di usare solo combinazioni lineari, si possono applicare funzioni di attivazione non lineari g(a)  per trasformare l’output:

y(x) = g(w^T x + w_0)

Esempi comuni:

    •    Gradino (output binario 0 o 1)

    •    Lineare con saturazione

    •    Sigmoide logistica g(a) = \frac{1}{1+e^{-a}} , utile per interpretare l’output come probabilità a posteriori

    •    Sigmoide simmetrica

Con probabilità condizionate gaussiane, la funzione sigmoide logistica permette di esprimere la probabilità di appartenenza a una classe.

4. Limiti delle Reti Neurali Monostrato

Le reti a strato singolo separano i dati con iperpiani, quindi non possono risolvere problemi non linearmente separabili, come lo XOR.

5. Reti Neurali Multistrato

Per classificare dati non linearmente separabili, si usano reti neurali multistrato, dove:

    •    Ogni livello trasforma le variabili del livello precedente con funzioni non lineari.

    •    Le unità nascoste (hidden units) aiutano a creare regioni di decisione più complesse.

    •    L’output finale è dato dalla combinazione delle attivazioni degli strati nascosti.

Le reti multistrato sono essenziali per problemi complessi, poiché possono suddividere lo spazio in regioni non lineari e risolvere problemi come lo XOR.